Computational Material Science

Computational Material Science

Computational Materials Science is a relatively new and rapidly evolving discipline that brings together elements from materials science, physics, chemistry, mechanical engineering, mathematics and computer science.

Charge density distribution in a silicon crystal

The reason for the strong demand for Computational Materials Scientist both in industry and academic research is manifold: properties of materials are not only determined by their respective chemical composition, but also to a large degree by their microstructure. Studying the interrelation between processing, structure and properties of materials is thus at the heart of materials science. The often competing, complex mechanisms take place on a range of different length- and time scales, requiring the development of new simulation methods suitable for scale-bridging. The investigation of crystal and defect properties for example, requires quantum mechanical calculations and atomistic simulation methods with typical time scales ranging from femtoseconds through nanoseconds and length scales ranging from Angströms to several hundred nanometers. Studying the interactions, statistics and self-organization of lattice defects on the so-called meso-scale requires methods able to adequately describe complex many-body problems over long time scales. On the macro-scale, finite-element models, which incorporate microstructure information using averaging constitutive laws, are used in the design of engineering structures and devices.

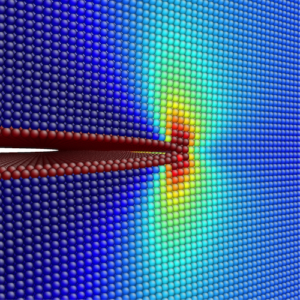Stress field around a crack tip in a nickel single crystal		Crack in a silicate glass

Students of the TAF Computational Materials Science will receive a solid foundation in materials science with a focus on mechanical properties. The TAF will provide them with conceptual foundations as well as with theoretical and numerical background knowledge required to perform state-of-the art materials simulations. Direct, hands-on teaching enables the students to build up their own “computational toolbox” with which they can address the most common tasks in computational materials science and engineering. Planning and conducting small research projects further fosters the students’ research competence.

Simulation of an experimental foam structure with very high porosity

Modeling and simulation are nowadays regarded as the third pillar of the scientific method, complementing theory and experiment. Modeling and simulation tools are thus finding increasing applications not only in fundamental materials-science research, but also in real-world design and optimization of new materials. Graduates in the field of Computational Materials Science find excellent job opportunities in academia and corporate research & development departments.

Courses in the Master program

Fundamentals of Materials and Material Structure

This course provides an introduction to materials science, starting with presenting the different classes of materials, their atomic structure, the different types of interatomic bonding and the arrangement of atoms in crystal lattices.
Further topics include

• defects in crystals (1D, 2D, 3D)
• mechanical properties of metals (basics)
• dislocations and strengthening mechanisms
• phase diagrams
• phase transformations in metals (basic nucleation theory, microstructure formation)
• structure and properties of ceramics
• corrosion

Fundamentals of Material Properties

The lecture enables the students gain an insight into the mechanical properties and behavior of materials used for engineering and technological applications. The course aims to bring together materials science and engineering perspectives towards understanding, design and application of materials. A high level of student involvement through presentations ensures hands-on participation in the course.
Topics include:

• Introduction to Tensors
• Elasticity
• Plasticity and failure
• Fracture mechanics
• Mechanical behavior of metals
• Fatigue
• Creep

Foundations of Computational Materials Science I & II

These lectures provide conceptual foundations and theoretical background knowledge for state-of-the art materials simulation. Topics include:

• Atomistic theory of matter – from electrons to interaction potentials
• Statistical mechanics of materials: equilibrium and non-equilibrium systems and ensembles
• Stochastic processes and stochastic modeling
• Coarse graining methods (how to pass from one scale to another?)
• Continuum models of materials and microstructures

Multiscale Simulation Methods I & II

These lectures provide a broad overview of simulation methods operating on length scales from the atomistic to the continuum scale. Methods introduced include Molecular Dynamics, equilibrium and kinetic Monte Carlo simulation, mesoscopic methods such as Dislocation Dynamics and the Phase Field method, and continuum-level modeling of materials behavior in Finite Element simulations. The introduction of methods operating on different scales is complemented by a discussion of multiscale approaches, i.e. the linking of models operating on different scales. This course is accompanied by practicals where the students will have the opportunity to numerically implement one-scale models in a hands-on manner. This will be complemented by examples of information passing between different scales and the construction of simple multiscale models.

Numerical Methods in Materials Science: Atomistic Modeling

The aim of the course is to build the theoretical basis required to perform and analyze cutting-edge atomistic simulations in materials science, and to provide the students with a “computational toolbox” for the most common tasks in atomistic modeling. The focus of this course lies on direct hands-on teaching. The students will work on multiple little projects related to current research topics. This will enable the students to independently perform simulations using classical molecular dynamics (MD) codes like IMD and QuantumEspresso for DFT calculations. Topics include:

• General theory of atomistic simulations
• Advanced methods for the generation of atomistic samples
• MD integration algorithms for different thermodynamic ensembles (NVE,NVT,NPT)
• Energy minimization algorithms and structure optimization
• Introduction to Density Functional Theory
• Determination of defect properties
• Atomic interaction potentials, including EAM, BOP and Tight-Binding Methods
• Advanced analysis and visualization methods for atomistic samples
• Monte Carlo and kinetic Monte Carlo methods
• Modeling thermally activated events: transition state theory, nudged elastic band calculations, hyperdynamics

Generalized Continuum Models of Materials with Microstructure

The behavior of materials with complex microstructures can not always be described by standard approaches of continuum mechanics. In particular, theoretical modeling of small scale plasticity with its associated size effects requires modification of conventional modelling approaches. The lecture shows how this can be achieved by using different generalizations of classical continuum models to account for account for microstructural heterogeneity and length scales, including

• Cosserat continua
• Micromorphic continua
• Nonlocal and gradient-dependent models
• Stochastic models of heterogeneous microstructures

Dislocation Theory and Dislocation Simulation

The lecture covers the foundations of dislocation theory (stress and strain fields, dislocation energetics and interactions) as well as dislocation-based modeling of plastic deformation processes, including both discrete and continuous simulation approaches.

Computer Lab

Practical experience in materials modelling and materials simulation, using C++ as programming language. Practicals can be chosen from:

• Molecular dynamics
• Monte-Carlo simulation and optimization
• Microstructure dynamics using the phase field method
• Plasticity modeling using dislocation models
• Finite Element plasticity
• Simulation of fracture processes

Each practical provides the student with a “toolbox” of programs and a research question. Task of the student is to assemble and adapt the necessary tools and to use them for investigation and analysis of a specific materials problem. Examples are typically taken from research work done during the past decade.

TAF-Betreuer